How to leverage Logseq's linked structure?

[alex0]

Are you aware that there is the Graph Analysis plugin, that among other things, let you color nodes using Simple Queries syntax?

Once you have tried all its options, isn’t that way more useful than the default one?

[Edit] My graph of real nodes (utility-pages hidden):

[Leo_Fan]

I have the same problem. The graph includes too much unrelated nodes, while lots of useful information is left out. I wonder if it’s possible to

1. build a subgraph with control of which notes are included, by means of a query
2. customize annotation of each note, mayby by a specific property
3. customize relation and placement of notes
4. represent the subgroup as a page or whiteboard.

I’m trying to take Zettelkasten notes in logseq. A graph of the notes will be of tremendous help to me.
If anyone familiar with developing plugin finds the features necessary, please try to implement them.

[Siferiax]

Nope because I’m on mobile 99% of the time so I don’t really use plugins.
I’ll give it a try on PC later. For this purpose I don’t mind trying plugins as it is not for every day use.

[Siferiax]

@Leo_Fan

I have the same problem. The graph includes too much unrelated nodes, while lots of useful information is left out.

My issue is not necessarily with the graph view per se. I’m just using it to illustrate in this case.
My issue is more broad, in the sense that, I do not know how to extract extra value from what I have regardless of the workings of the graph view.

@Leo_Fan

If anyone familiar with developing plugin finds the features necessary, please try to implement them.

Have you tried the plugin @alex0 mentioned?

[Leo_Fan]

Yes, my concern is more about a specific use case. I have tried graph analysis. It lacks features 2~4. I’m trying to manage whiteboards manully, for now.

[mentaloid]

When graphs can talk

For having a visual graph communicate something to us, we should consider its signal and noise:

• Each connection between nodes:
  • carries some signal
  • adds noise to the nearby connections
• That makes a graph (or subgraph) with:
  • too few connections: silent, has nothing to say
  • too many connections: noisy, has nothing meaningful to say
• As a (simplified) consequence, graphs (or subgraphs):
  • that look like stars (or stars of stars), are neat but silent
  • where everything connects with everything else, are noisy
  • that combine the above, combine silence with noise
  • that balance their connections, may communicate something
• To improve the situation:
  • look for nodes that are:
    • underconnected:
      • have less than 2 connections
        • they should either:
          • acquire more connections
          • be merged into other pages
    • overconnected:
      • have more than 8 connections
        • they should remove some connections by either:
          • delegating them to the remaining ones
          • breaking into smaller pages
      • bridge things that are directly connected to each-other
        • this adds noise
        • decide which are the direct connections and remove the indirect ones
  • use the following soft rule to add missing connections or even nodes:
    • if node A has:
      • a connection of type R with node B
      • a connection of type S with node C
    • and R is orthogonal to S
    • then some node D has:
      • a connection of type S with node B
      • a connection of type R with node C

---

Structure matters

A graph is a (multidimensional) map.

The streets on a map originate from either:

• animals (e.g. in an old forest)
  • they connect points of interest (water etc.)
• engineers (e.g. in a modern city)
  • they essentially connect doors

They both are useful in going from one point to another.

• If I structure a graph as:
  • an index, it will be easier to find the inserted info
    • think of multiple doors in parallel corridors
  • a hierarchy, it will be easier to navigate that hierarchy
    • think of narrow streets connecting to larger ones, to avenues, to highways
• Structures like the above, give me back exactly what I put in.
  • This is great for returning to a place.
• If I let a graph structure itself, it may give me back more, both:
  • from its structure
    • think of ants’ tracks
  • from its lack of structure
    • It is a comparison between expectations and the actual graph.
      • Whenever the expectations fail and they are:
        • right, it is a chance to fix the graph
        • wrong, it is a chance to learn something

---

A simplified example

• Consider a single journal-note:
  • [[Purchase]] of [[apples]] by [[my neighbor]].
• Here are some easy questions I could ask, related to that note:
  • What did my neighbor purchase?
  • Who did purchase apples?
  • What happened between apples and my neighbor?
• Here is a less easy question I could ask:
  • What are the transactions between persons and fruits?
• To answer that, some extra knowledge is needed:
  • my neighbor is a person
  • an apple is a fruit
  • a purchase is a transaction
• But I still query for pre-existing notes:
  • I entered some transactions in the past.
  • I query for those transactions in the present.
  • This is the traditional boring approach.
• Now consider a graph that contains no transactions at all.
  • This is not a necessity, but helps with focus.
• Then consider the following hard question:
  • What could my neighbor be involved in?
• And here is a desired answer:
  • My neighbor could purchase apples.
• The desired answer doesn’t exist in any individual note.
  • I query for possible transactions in the present.
  • I may enter those transactions in the future.
  • I may find that some have already happened in the past, but I missed them.
• To provide such an answer, even more knowledge is needed:
  • a person is an agent
  • a fruit is an object
  • a transaction involves an agent and an object
    • this is the type of knowledge that can lead to discoveries
• One could try working this answer by combining the previous knowledge:
  • my neighbor is a person, therefore an agent
  • apple is a fruit, therefore an object
  • a purchase is a transaction, therefore involves an agent and an object
  • Datalog anyone?
• Alternatively, one could work this answer by following connections in a well-made graph:
  • There is a path from my neighbor to purchase.
  • There is a path from purchase to apple.
  • Nobody constructed those paths on purpose, they emerged.
  • In a noisy graph, they remain invisible.

---

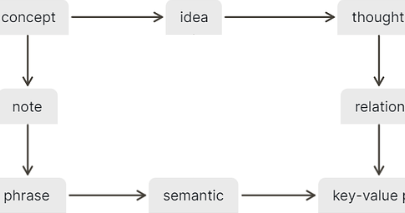
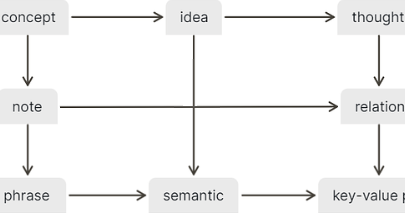
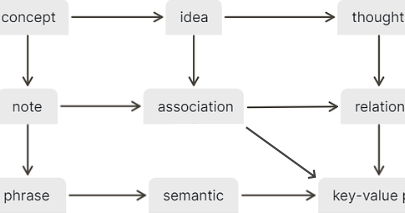
A simple visual example

• Visit A whiteboard for the main concepts in Logseq
• Imagine any of the nodes missing, either:
  • along with its connections to its neighbors:
    
  • with its neighbors connected directly:
    
  • even if the remaining nodes have issues
    • e.g. association instead of relation
• Or imagine a mistaken connection:
  
• Wouldn’t it be easy to visually detect any of those issues?
  • This is possible because of the emerged pattern.
• Is everything that easy?
  • Not at all, but you have one more tool, if you want to use it.

---

Short points to keep

• The right tool for the job:
  • Journals are for events.
  • Other pages are for knowledge.
  • It is not “one or the other”, both can co-exist.
• Graphs don’t benefit from journals, but from interlinked pages.
  • Tagged journals generate stars.
    • We typically hide those.
  • Interlinked pages generate paths.
    • Excessive noise makes paths invisible.
  • Therefore, graphs don’t benefit from stars, but from visible paths.
• Failed expectations can be:
  • opportunities
  • pleasant surprises

[Siferiax]

@alex0

[Edit] My graph of real nodes (utility-pages hidden):

I didn’t want to go through my entire graph to hide certain pages and I also don’t think it would add much, because this is what it looks like

Basically everything still looks connected to everything

@mentaloid

For having a visual graph communicate something to us, we should consider its signal and noise

@mentaloid

too many connections: noisy, has nothing meaningful to say

I think this would illustrate the problem for me pretty well. I created a new graph with some (based in reality) sample pages and connections.

Projects & Areas as per the PARA method. Connected nodes have tags:: Projects or tags:: Areas.
projectNameHere has the properties as follows:

tags:: Projects
area:: Home
subject:: roomName

A project is a project and relates to a specific area and has a specific subject. In this case the real project relates to some home remodeling of a specific room

Then as per the Bullet Journal method I have a monthly page.
In my real graph this would have all my weekly information (agenda, goals, highlights) and my monthly goals & highlights.
For this sample it is filled with just the basic:

These types of connections show up in my actual graph as well.
Goals are only added to these pages. Highlights is a bit tricky.
For example say I played Tunic on Monday, Friday and Sunday. I will have journal events for this on each of those journal pages. Then for that week I would have a highlight “Played Tunic” and then also for the month I’d have a highlight “Played Tunic”.
I don’t like this approach honestly. And it is a dilemma I have between a weekly/monthly overview of the journal events I find important and having all these extra connections.
Alternatives:

• Use block references
  • but which block then in the example I gave? the Monday one?
• Use queries
  • when returning blocks I would have all three events
  • when returning pages, for games this works, for other events I’d lose the context.
  • when returning :block/content only, it doesn’t always use distinct correctly
• ??? some other method?

As you can imagine a lot of the mess of my graph is due to this. A lot of connections go to either a PARA method specific page, or a month specific page.

• Would I have to go through every month specific page and exclude it from the graph?
• Or is there a better method to my madness
• Should PARA pages be included or excluded?

For my games I use:

area:: Hobby
subject:: games

Maybe this is redundant? Should it only be subject:: games? I think that would be the correct hierarchy, instead of using area as games has not been specified as a specific area, but is part of the Hobby area.

This graph looks already better I feel.

So this should improve the noise ratio of my graph. Is this a good approach I should consider doing with my actual graph?

@mentaloid

Therefore, graphs don’t benefit from stars, but from visible paths.

I guess the improved graph follows this logic more.

@mentaloid

underconnected:

• have less than 2 connections
  • they should either:
    • acquire more connections
    • be merged into other pages

I feel that is not necessarily true for something like my notes on specific games. Due to the volume of notes it makes sense for a game to have its own page. But it’s not going to be connected much beyond that unless I find some reference to another game or something like that?

@mentaloid

overconnected:

• have more than 8 connections
  • they should remove some connections by either:
    • delegating them to the remaining ones
    • breaking into smaller pages

This is the problem that occurs with my month pages, as most things get connected to at least 1, but often multiple month pages. Hence I wonder if Month pages should be built differently entirely, or should they merely be hidden from the graph?

@mentaloid

bridge things that are directly connected to each-other

• this adds noise
• decide which are the direct connections and remove the indirect ones

I believe you mean the Hobby > games > Tunic > Hobby thing here. I agree.
It should probably just be Hobby > games > Tunic

@mentaloid

use the following soft rule to add missing connections or even nodes:

• if node A has:
  • a connection of type R with node B
  • a connection of type S with node C
• and R is orthogonal to S
• then some node D has:
  • a connection of type S with node B
  • a connection of type R with node C

Can you give a more concrete example? I can’t quite wrap my head around this one.

@mentaloid

• Structures like the above, give me back exactly what I put in.
  • This is great for returning to a place.
• If I let a graph structure itself, it may give me back more, both:
  • from its structure
    • think of ants’ tracks
  • from its lack of structure
    • It is a comparison between expectations and the actual graph.
      • Whenever the expectations fail and they are:
        • right, it is a chance to fix the graph
        • wrong, it is a chance to learn something

Going by your analogy I think my graph is for the most part structured like a hierarchy. Door Tunic on street games connected to road Hobby in town Areas. So I wonder how do I do this differently? If that could be beneficial. How would I have the graph structure itself?

@mentaloid

A simplified example

You kind of lost me here. I mean I follow what you’re saying in theory, but I don’t quite understand what that would look like in practice?

@mentaloid

The right tool for the job:

• Journals are for events.
• Other pages are for knowledge.
• It is not “one or the other”, both can co-exist.

Agreed. And I recently ran into a conflict. Consider the “logbook” (not the Logseq one!) where would that live?

• In the journal
  • It is what I did in a game on a certain day
• On the page for the game
  • they are notes for the game and it can be useful to have all of them in one place
  • linked references also contain other links and so the notes may not be as easy to read that way.

It’s not just games, but also something like therapy sessions.
I had this on my journal pages, but referencing the logbook became difficult when I wanted to read/see the timeline to reflect on it. So I started putting in a Logbook block with links to the journal pages and under the reference blocks with my notes.

- ## Logbook
  - [[journal]]
    - note

I feel there could be reasons for either approach in this case. I feel it is a bit of a gray area. However for me to get value out of this logging I do, I need it to be together.

I talked a lot about games, because I feel this is the most direct example and similar to other daily uses (for example a bike ride, or art).
However there is also some actual knowledge stuff in there which is to say articles I read with my notes in them.

Having typed all this… I guess the two main structural questions I’m dealing with are:

• is the PARA method structure a good framework for me?
  • should I hide the PARA pages in my graph?
  • should I do things differently? if so, in what way?
  • PARA just seemed useful for organizing things in 4 broad categories and letting all other structure emerge from that.
  • It prevents me from falling into the trap of a very granular hierarchy structure. (which is what I had with files and folders in the past)
• how do I structure my monthly overview pages in a useful way?
  • should I hide these from my graph?
  • or should they be completely different so they won’t show up in the first place?

[mentaloid]

@Siferiax

is the PARA method structure a good framework for me?

Better than nothing, but weak.

@Siferiax

A project is a project

Rather a PARA project is a project.

@Siferiax

For example say I played Tunic on Monday, Friday and Sunday.

This type of information is hardly useful in anything other than statistics.

@Siferiax

Should PARA pages be included or excluded?

should I hide the PARA pages in my graph?

should I hide these [agenda, goals, highlights] from my graph?

should they merely be hidden from the graph?

Having to question it that much, it’s a yes, hide them to reduce the noise.

@Siferiax

Maybe this [area + subject] is redundant?

Yes, it is redundant. Both in games and in projects.

@Siferiax

I feel that [more than 1 connection] is not necessarily true for something like my notes on specific games. Due to the volume of notes it makes sense for a game to have its own page. But it’s not going to be connected much beyond that unless I find some reference to another game or something like that?

Cannot “leverage Logseq’s linked structure” without enough links. Linked knowledge on a game could be elements of its genre, reasons that you play it, any lasting effects on you, etc. Think of a wiki on either the game itself (like those found online) or the game in relation to you (few games are more than time-killers). Days and hours don’t make for interesting articles.

@Siferiax

I believe you mean the Hobby > games > Tunic > Hobby thing here. I agree.
It should probably just be Hobby > games > Tunic

Yes, triangles are the smallest case of “everything connects to everything else”.

@Siferiax

I follow what you’re saying in theory, but I don’t quite understand what that would look like in practice?

This is for homework, to see how the paths emerge.

@Siferiax

I think this would illustrate the problem for me pretty well.

Your illustrations help indeed.

@Siferiax

This graph looks already better I feel.

I guess the improved graph follows this logic [paths] more.

It does. Well done.

@Siferiax

So this should improve the noise ratio of my graph. Is this a good approach I should consider doing with my actual graph?

These are steps to the right direction. Clarity gets improved gradually. Here are some more steps in moving from indices to concepts:

• make them singular, e.g. game
• remove capitalization, e.g. home

Could look like this:

@Siferiax

Going by your analogy I think my graph is for the most part structured like a hierarchy. Door Tunic on street games connected to road Hobby in town Areas.

…in PARA land. True. And that facilitates navigation, but not discoveries.

@Siferiax

Can you give a more concrete example? I can’t quite wrap my head around this one [the soft rule].

• Being primarily hierarchical (i.e. items inside groups, say R), your connections are rarely orthogonal, e.g.:
  • item roomName (say A) connected (R) to group home (B)
• Consider another relation (S orthogonal to R) about instances of concepts:
  • instance roomName (A) connected (S) to concept room (C)
• The soft rule says that there is another node (D) between home (B) and room (C):
  • home (B) could be an instance (S) of house (D), where room (C) is an item (R)
• Is this new knowledge?
  • New knowledge doesn’t emerge every day but:
    • when it does, it does in ways like that
    • understanding given knowledge can also be like that
• Now if you acquire knowledge on:
  • room decoration, you can apply it on roomName
  • house remodeling, you can apply it on home
• Isn’t this superficial?
  • Enough to serve as a simple example.
  • There is no difference in how things emerge from:
    • the bottom of a glass
    • the bed of an ocean

@Siferiax

I never found anyone concretely explaining what they mean with it

Hopefully the above is concrete enough.

[Siferiax]

@mentaloid

Better than nothing, but weak.

@mentaloid

Rather a PARA project is a project.

I get what you’re saying here. Especially in the context of the rest of your comments. It makes me rethink my entire structure/graph.
Not necessarily to throw it out the window entirely, but more so in the assumptions made and execution of my structure. So I will have to consider and revisit this as I work on creating a better graph.

@mentaloid

This type of information is hardly useful in anything other than statistics.

Agreed. It has been something that’s been bothering me on some level. (why do I even log this) And at the same time I do love my statistics. So then the question becomes, what exactly do I need for those statistics and what does that look like in the bigger picture.
This makes me ponder bigger question on my assumptions, as already stated. I will have to give this more thought.

@mentaloid

Having to question it that much, it’s a yes, hide them to reduce the noise.

That does improve things significantly

I think this is a better starting point to work on this more. (Redundant connections for example)

@mentaloid

Yes, it is redundant. Both in games and in projects.

Ah! I didn’t immediately recognize it for projects, but seeing your example below totally made that clear to me.
One more item to add to the possible improvements list

@mentaloid

Linked knowledge on a game could be elements of its genre, reasons that you play it, any lasting effects on you, etc.

This was such a revelation in all its glorious obviousness! I had never thought about it in these terms/possibilities!
Thank you for this. It gives a whole new perspective.

@mentaloid

Days and hours don’t make for interesting articles.

Very true!

@mentaloid

• make them singular, e.g. game
• remove capitalization, e.g. home

Making them singular reminds me of my work standards in regards to table naming conventions so yeah I see that one clearly. Though it makes me wonder about the page itself
My games page has an overview of my games (through queries). I guess maybe it doesn’t matter so much whether that is named games or game.

As for capitalization… yeah my graph is very inconsistent there. I never gave it much thought when I should have.

@mentaloid

Could look like this

Really helps make some things clear. Thanks!

@mentaloid

…in PARA land. True. And that facilitates navigation, but not discoveries.

I guess this is very true. And maybe why I ran into my dissatisfaction.

@mentaloid

Hopefully the above is concrete enough.

YES! that whole section cleared up so much and gave a lot of things to ponder about. Thank you.

I will give your post more thought and see about slowly improving my graph.

[Siferiax]

@mentaloid

The soft rule says that there is another node (D) between home (B) and room (C):

• home (B) could be an instance (S) of house (D), where room (C) is an item (R)

So I was just working on the graph a bit… and… something just clicked into place, in my brain.
I was considering/testing out a structure of type:: and cluster:: (I didn’t like the part-of type naming).
So I was going through my projects.
type:: project, cluster:: hobbyroom
Page hobbyroom type:: room, cluster:: appartment
Page appartment type:: house
Page room cluster:: house
Then I came to another project…
type:: project, cluster:: livingroom
Page livingroom type:: room, cluster:: appartment…
Oh snap! I’m building a house or put another way, these projects are now actually linked, directly and logically.

[mentaloid]

• You are essentially modelling your understanding about a part of reality.
  • This process can actually refine your understanding.
  • Given that reality is huge, should not aim for completeness. It is both:
    • impractical: noise
    • impossible: Gödel
  • If you want a detailed model of your house:
    • put it in its own graph
    • then share (currently copy) selected pages to graphs that need them
• I would not say that:
  • “some project has some cluster”
    • Consider target or object.
  • “projects are linked directly”
    • we don’t want that (noise) to begin with
    • there is just a path of links between them

[Siferiax]

@mentaloid

Given that reality is huge, should not aim for completeness.

Indeed not. I’m just trying to see the possibilities as well as trying things out. And definitely no more than necessary.

@mentaloid

I would not say that:

• “some project has some cluster”
  • Consider target or object.

I’m trying to use a general structure (maybe that is wrong?) to classify pages.
Something belongs to something else, either hierarchal or in context.
To give some more abstract examples, writing on my blog is part of writing. Buying a new freezer is part of my physical inventory (which would relate to my house eventually).
Doing my taxes is part of my finances.
I wish to avoid making a new property key for every little thing. Only doing so when it adds some extra value. In this case cluster is always to mean the page is part of this collection/other page/give it a name.
Now that I think on it, I guess the “part of” falls apart a bit when looking at it from a project perspective.
It was also something I was questioning when trying to classify a treatment I had. In so much that I have a page dedicated to my personal experience of said treatment, and a page that is dedicated to an article about that treatment (reference page). And I was unsure how to define their relationship. It is not that my experience is part of the article or vice versa. Nor is the article a type of the experience or vice versa. So my “standard” links so to speak don’t apply here. There is a relationship however.
So I was thinking of a more “natural” link. Something like “[article]([[pagename]]) with further information about this treatment”.

@mentaloid

I would not say that:

• “projects are linked directly”
  • we don’t want that (noise) to begin with
  • there is just a path of links between them

I just meant directly as in there is a path between the two projects. Specifically it made me realize I have two projects related to my house. Where this link was not so directly/obviously/logically present before.

[mentaloid]

@Siferiax

to classify pages

• “Forget” about classifying.
  • That leads to hierarchies.

  • Classification is just one of multiple types of relationships.

• Think about relating or rather associating.
  • That leads to graphs.

@Siferiax

I’m trying to use a general structure (maybe that is wrong?)

• Using a single property to generalize relationships that are:
  • genuinely similar, is ok
    • can simplify the graph
      • although similarities should be supported by the system
  • non-similar (i.e. orthogonal), is not ok
    • Among other issues, it prevents discoveries.
• belonging fits with group and cluster or part of, but doesn’t fit with type
• is fits with type and class or instance of, but doesn’t fit with group
• The relationship between a treatment and an article doesn’t fit with either.
• The relationship between a room and a project also doesn’t fit with the first two.
  • What belongs to what?
    • The project to the room?
    • The room to the project?
    • None, they have a different type of relationship.
• The last two may fit together:
  • The project may target the room.
    • The room is the object of the project.
  • The article may target the treatment.
    • The treatment is the subject of the article.
      • Yeah, in English subject may mean object…

[Siferiax]

@mentaloid

“Forget” about classifying.

• That leads to hierarchies.

Oh! Well that’ll be a challenge/shift in mindset

@mentaloid

Think about relating or rather associating.

• That leads to graphs.

Would that be more in the sense that “I happen to have this page and that page and they happen to be related”? Rather than “I have this page and it relates to”?
In other words would I already predefine relations or would they only be made when I have two pages I can relate.

To stick with an earlier example. Suppose I make a project page for my hobbyroom. This is the first page of my graph that I make. So there is no relationship yet. Then later on I make a project for my livingroom. This relates to hobbyroom in the sense that they are 2 rooms in the same house. I could relate both to being part of my appartment. They would now have a path between them.
So in this question, when is this path made? Is hobbyroom at time of inception related to appartment. (The relationship with livingroom is not made deliberately) Or is this relation made in response to the creation of living room. (The relationship is made deliberately)
If the former, what relationship do we define at the moment of page creation? Those we know? But that could potentially lead to trying to model all of reality. Just one? The most significant in the context?
The latter would require deeper thought, but also relying on memory.

@mentaloid

Using a single property to generalize relationships that are:

• genuinely similar, is ok
  • can simplify the graph
    • although similarities should be supported by the system
• non-similar (i.e. orthogonal), is not ok
  • Among other issues, it prevents discoveries.

I suppose it makes sense that should I query all types, but I get results that are not actually types but something else that would muddy the waters.

Still I guess for me it is a big mindshift to not need to have everything very strict and “one way”
That’s gonna take some work to get around because I do feel it would be valuable in the end.

[mentaloid]

@Siferiax

would I already predefine relations or would they only be made when I have two pages I can relate

Just make sure that nothing is dangling, i.e. that:

• everything has a minimum of 2 connections
• your map has no dead-ends, you can:
  • navigate everywhere without going back
  • visit your nodes in multiple sequences
    • these are the paths that may “click things into place”
    • this is how the mind:
      • navigates inside the brain
        • therefore the mindshift should feel familiar and come natural
      • leverages the brain’s linked structure
        • thus the simplest of brains can be superior to dumb datacenters

@Siferiax

what relationship do we define at the moment of page creation?

• Try thinking of something relevant to your specific graph.
• If not, fall back to one of the basic relationships (is and has or similar).

[Siferiax]

These are some great rules of thumb to keep in mind thanks.
It’ll be tricky… but maybe it will resolve itself as I work on making my graph better.

So as I’m working on it, my graph right now looks like this:

Lots of connections are (right now) deliberately broken, so it make sense lots of things just “float around”.
I have worked on removing all the triangle connections from the hobby page (blue dots).
The dark blue star is my games page with all the games connected to it.
I’m pretty happy with my progress, but I’m far from done

Anyway I ran into an interesting question. About my cats
So I have 3 pages. 1 with information related to both cats and then 1 page for each cat with their personal information. For example I want to track which cat puked when, so in the journal I would have [[Rox]] puked, probably because of reason.
In the cats page I would have the recurring tasks like food prep or clean the litterbox. And in the journal when it is about both cats, I’ll use that page reference as well. Took the [[cats]] to the vet.
Now I have a project related to my cats. Therefore I want to link this project to the [[cats]] page. While on the project page I might reference [[Rox]] and [[Sky]] individually as well.
This would create a triangle. (after all [[Rox]] is one of my cats and thus a link between his page and the [[cats]] page exists)
In such cases would it then be better to be more specific and not use the [[cats]] page? Both in the journal and the project.

[mentaloid]

• Sounds like page cats is a (longterm) project itself.
  • If so, consider renaming it to something like cats project
    • This should break things like Took the [[cats project]] to the vet
    • Should also move any non-project content to a page cat (singular)
• If the other project is:
  • the same: merge them
  • different:
    • don’t connect it to cats project
    • link only to each cat individually
• Instead of Took the [[cats]] to the vet, write Took {{cats}} to the vet
  • {{cats}} should be a one-time macro defined like this:
    • :cats "<div class='kit' data-kit='expandmacro'>[[Rox]] and [[Sky]]</div>"
  • that immediately expands to: [[Rox]] and [[Sky]]

[Siferiax]

@mentaloid

Instead of Took the [[cats]] to the vet, write Took {{cats}} to the vet

• {{cats}} should be a one-time macro defined like this:
  • :cats "<div class='kit' data-kit='expandmacro'>[[Rox]] and [[Sky]]</div>"
• that immediately expands to: [[Rox]] and [[Sky]]

Need to learn macros! This sounds really helpful. It would definitely solve this issue more thoroughly.
Edit: Got it working

We were talking earlier about octogonal connections. So I found this charming cluster in my graph:

• References (aka. articles or videos)
  • Introduction to the Zettelkasten Method
  • Folgezettel is More than Mechanism
  • Progressive Summarization
• Subjects
  • Logseq (this page is a bit cluttered and I need to come back to it)
  • Zettelkasten
  • PKM
• Project / my own stuff
  • Mijn notitie systeem

To declutter, thinking on what we discussed. It seems to me that

• Zettelkasten should link to PKM (it is a PKM system)
  • Therefore the two articles on Zettelkasten would link to Zettelkasten instead of PKM, a more specific relationship.

However this cross relationship would still exist.
In “Introduction to the Zettelkasten Method” I mention both “Folgezettel is More than Mechanism” and “Progressive Summarization” in my notes about this article.

• “[[Zettelkasten]] is more work upfront than [[Progressive Summarization]]. It requires more effort and pre-planning. On the other hand it also creates more value up front.”
• “There is more to it than that, see [[Folgezettel is More than Mechanism]]” (in response to the article’s explaination of Folgezettel)

I feel these are fair relationship. Would this result (the triangles) in this case be ok, or am I missing something important?

[mentaloid]

@Siferiax

am I missing something important?

When an article is not about outlining a single concept:

• its main text should be treated like an external pdf or even picture file:
  • It should be kept clean, not participating in the connections of the graph.
  • If it contains knowledge about an association, that should be copied to the appropriate page.
  • If it combines knowledge from other pages, its should embed that as not being its own.
  • It could still contain web links etc.
• its own associations (and not of its content) should be in dedicated notes or properties, apart from its main text

[Siferiax]

I don’t follow, I’m sorry.
These are pages with my notes about these articles.
So the main article text is not on the page except for citations I want to keep. All citations don’t contain links.
All notes I make do contain links.
The page is about a certain subject, so it is linked to said subject.

So here’s basically what happens. I have read the article “Introduction to the Zettelkasten Method” (article 1). I copied some highlights into Logseq and made some additional notes for myself. I gave the page subject:: Zettelkasten.
Later I read the article “Folgezettel is More than Mechanism” (article 2). I did the same for this article, highlights, notes and subject:: Zettelkasten.
Later I was reviewing (for one reason or another) my notes on article 1 and it made me think of what I read in article 2.
This let me to write the note on the page of article 1. “There is more to it than that, see [[Folgezettel is More than Mechanism]]” In response to the citation about the unique id used in Zettelkasten.

This leads to connections between both articles and each to subject Zettelkasten.
What in your opinion should it look like instead?